No structure, even an artificial one, enjoys the process of entropy. It is the ultimate fate of everything, and everything resists it.

- Philip K. Dick

ENTROPY DEFINED IN STATISTICAL MECHANICS

Generally there is a misconception around entropy, in the public domain and general discourse, which is that, it is disorder or chaos (philosophical position is different from scientific one's) which is not that simple. In any peer group you may have listen many things about entropy , many people refer entropy purely as disorder which is not that case, it is a scientific concept not philosophical one

To understand entropy as a scientific concept you have to look at its origin which is in thermodynamics. In thermodynamics entropy is used or defined at 2 levels mainly microscopic and macroscopic.

1. Microscopic- study of thermodynamics at atomic , molecular and nuclear level.

2. Macroscopic- study of thermodynamics at laboratory , terrestrial and atomic level.

To understand entropy, let's take a look at how it is mathematically defined at micro-level (by statistical mechanics ):-

To understand it, we have to take a look at the knee topics of statistical mechanics, which is micro-stats.

MICROSTATES

You might be thinking what this micro-state means ? Let me try to explain it to you by a simple analogy.

Suppose we have a system which consists of 3 particles which are distinguishable from each other labelled as A,B & C respectively.

Now let us say the total energy of the given system is given as 5H. It means that 5H energy is distributed over 3 particles in this particular system. Now let us assume that each particle can occupy a specific amount of energy, say 'nH' ( n times H) where n belongs to natural numbers (n=1,2,3.....)

Now keeping in mind the above assumption, let us try to guess what can be the possible individual energy of each particle? So it comes out to be, that there can 6 be possible cases as shown in the figure below

These are the 6 possible arrangements and they are called as microstates of any system and equal to Omega, so in this case Omega will equal to "6" and entropy will be :-

S=k ln(6)

DEFINITION OF ENTROPY

Let say in the above example total energy of system is 3H then there will be only one possible configuration which is A=H , B=H and C=H hence here S=0 as ln(1)=0, So what does these above two examples want to tell you about the nature of entropy, if you see in the first example the no. of microstates is High which gives result as higher entropy in comparison to 2nd one which had only one possible microstate, so from here, we can conclude that :-

" More the number of microstates, more the system is being disordered, hence more the entropy is, and vice versa also true"

Also in the above example, we have taken a very important assumption, which is that any microstate can have an equally likely possibility to occur, this assumption is also known as Fundamental assumption of statistical thermodynamics.

Now coming back to entropy, the equation we discussed above is important to understand the nature of entropy, but it is not used generally to calculate entropy, the actual equation which we use is :-

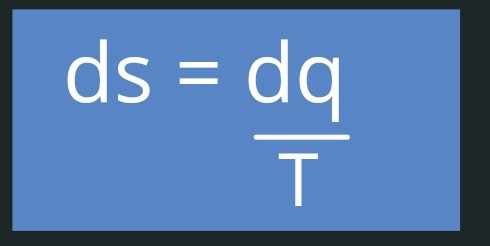
This is particularly used at the macroscopic level where we use variables like Temperature, pressure and volume. This is what entropy actually means, at microscopic level.